In introductory courses such as chemistry, economics, political science, and psychology, many relationships are represented graphically. You will often use graphs to make interpretations about what is happening in a relationship or construct graphs to describe an economic relationship.
While the examples below are taken directly from different economics textbooks, they demonstrate the kinds of skills that you will be required to use in many non-math introductory courses.
|
FIGURE 1: An individual buyer's demand curve for corn An individual's demand schedule graphs as a downsloping curve such as DD, because price and quantity demanded are inversely related. Specifically, the law of demand generalizes that consumers will buy more of a product as its price declines. Adapted from: McConnell, C. R. & Brue, S. L. (1996) Macroeconomics: Principles, problems and policies (pp. 40 & 41). New York: McGraw-Hill. |
Figure 1 above shows an individual buyer's demand curve for corn. From this graph you should be able to determine the price per bushel for any given quantity demanded (in bushels per week). To do this you must be able to correctly plot points on a graph.
|
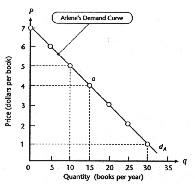
FIGURE 2 An Individual's Demand Curve for Paperback Books Arlene's demand for paperbacks can be shown by a curve or a schedule. Demand reflects an individual's willingness to buy various quantities of a good at various prices. A demand curve's negative slope reflects the law of demand, in this case, Arlene's buys more books at lower prices. Adapted from: Byrns, R. T. & Stone, G. W. (1995) Microeconomics (p. 63). New York: Harper Collins College Publishers. |
Figure 2 above shows another demand curve for price versus quantity. Again, you will need to be able to determine, for example, what the price of books will be if the quantity is 10. This involves using the graph skills presented in this section.
The skills you will learn in this section are:
 |
 |
| [table of contents] | [next unit] |