Linear Relationships

One of the most basic types of relationships is the linear relationship. Many graphs in introductory courses such as chemistry, economics, political science, and psychology will display linear relationships, and you will need to use graphs to interpret what is happening. There are several components of relationships that can be quickly determined from a graph once you know what to look for.

Below are examples taken directly from different economics textbooks. These examples demonstrate the types of skills you will be required to know and use in many non-math introductory courses.

Example

FIGURE 1: Graphing the inverse relationship between ticket prices and game attendance. Two sets of data which are negatively or inversely related, such as ticket price and the attendance at basketball games, graph as a downsloping line. The slope of this line is -1.25 Adapted from: McConnell, C. R. & Brue, S. L. (1996) Macroeconomics: Principles, problems and policies (p. 15). New York: McGraw-Hill.

Figure 1 above shows the relationship between ticket prices and attendance. From this graph you can see that this is a linear relationship where attendance will go down as ticket prices go up. This graph allows you to determine how much you should charge for a ticket. Using this graph involves an understanding of linear relationships and how to graph equations of straight lines.

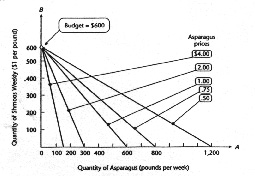
FIGURE 2: Budget lines for $600 income with various prices for asparagus. All else being equal, as the price of asparagus falls, the budget line expands and becomes less and less steep. This reflects the declining price of asparagus relative to its alternatives. Alternatively, as the price of asparagus rises, less and less can be purchased if the entire budget is spent on asparagus. Adapted from: Byrns, R. T. & Stone, G. W. (1995) Microeconomics (p. 143). New York: Harper Collins College Publishers.

Figure 2 above shows a more complex relationship involving prices of asparagus and budget lines. Here we can see how the price of asparagus affects the quantity of different foods that can be purchased. Understanding this relationship and what this graph shows involves using the graph skills presented in this section.

The skills you will learn in this section are:

• Draw a graph from a given equation.
• Determine whether a given point lies on the graph of a given equation.
• Define slope.
• Calculate the slope of a straight line from its graph.
• Be able to identify if a slope is positive, negative, zero, or infinite.
• Identify the slope and y-intercept from the equation of a line.
• Identify y-intercept from the graph of a line.
• Match a graph with its equation.

[table of contents]	[next unit]