1. Generate a list of points for the relationship.

   You should have created a table to obtain some points. A sample using 0, 1, 2, and 3 for x is shown in the table. To obtain y values, plug the x values into the equation y = 2x + 10 and compute.

   x y 0 10 10 30 20 50 30 70

   x = 0 y = 2 (0) + 10 y = 0 + 10 y = 10

   x = 10 y = 2 (10) + 10 y = 20 + 10 y = 30

   x = 20 y = 2 (20) + 10 y = 40 + 10 y = 50

   x = 30 y = 2 (30) + 10 y = 60 + 10 y = 70

   The points that we have defined here are:
   

   (0, 10), (10, 30), (20, 50), (30. 70)

Draw a set of axes and define the scale. This part was done for you in the problem. Copy the axes provided in the practice problem. Plot the points on the axes. Next, plot the following points (0, 10), (10, 30), (20, 50), (30. 70) on a set of axes. NOTE: Regardless of the points you selected, your graph of the line will still be the same. Draw the line by connecting the points. Once you have plotted the points, connect them to get a line.

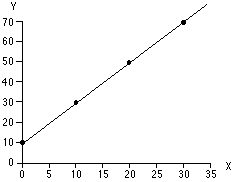
What if your graph does not look like this?
If your graph does not look like the one shown here, read through the suggestions below to determine where you may have made a mistake.

If any of your points do not lie on your straight line:

• Check your calculations for an error in computing y values. Check our calculations to be sure they are correct.
• Remember that points are given in the coordinate notation of (x, y), with x first and y second.
• Check to be sure all of your points are plotted correctly.

IMPORTANT: You should always plot at least three points before drawing your line. This serves as an extra check because if one points does not lie on your line, you made a mistake somewhere.

If you understand this solution, then move into the next unit. If you still do not understand how to graph the equation of a straight line, you may need more review than is offered by this book. If this is the case, please speak with your professor for suggestions on how to get help.

[review unit]	[table of contents]	[next unit]