1. In the graph below, the straight line B is given by the equation y = Tx + P. If the line shifts from this initial position B0 to a new position of B1, what must have changed in the equation?
   
   • In this graph, the line shifted down but did not change its slope.
   • "P" is the y-intercept. If you extend both lines to the y-axis, you will find B1 intersects the axis at a smaller number. Therefore, the constant "P" changed in the equation. It also must have decreased.
   • "T" is the slope of the line. Since the slope did not change, the constant "T" remains the same.
2. In the graph below, the line A is given by the equation y = Z + Wx. If the line shifts from this initial position A0> to a new position of A1, what must have changed in the equation?
   
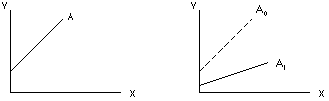
   • In this graph, the line has changed in steepness which means the slope must have changed.
   • Also, we can see that the y-intercept changed when the line shifted.
   • "W" is the slope of the line. Since the slope must have changed, the constant "W" must have changed.
   • Since A1 is less steep than A0> , "W" must have decreased.
   • "Z" is the y-intercept. Both lines are shown intersecting the y-axis. Since they do not meet the y-axis at the same point, the y-intercept must also have changed.
   • A1 meeting the axis at a smaller number. Therefore, the constant "Z" must have decreased as the line shifted.

If you had problems with this question, please revuew this unit again and then do the additional practice for this unit.

[review unit]	[additional practice]	[table of contents]	[next unit]